Three-Dimensional Sudoku Thesis

After a very busy spring semester, filled with Esports competitions, band concerts, and a senior thesis. I’m happy to finally have some time to write another blog post, this one offering up a quick look at my completed senior thesis.

Albion College Prentiss M. Brown Honors Thesis

As part of the requirement to graduate from Albion College with Honors, I had to attend four semester-length classes on varying subjects and draft a written thesis on a subject of my choosing.

I have adored puzzles and games for as long as I can remember. Whether it was building enormous LEGO® sets, solving extreme dot-to-dot puzzle books, or just playing strategy games, I always had a puzzle to solve. This is largely where I find my love for computer science too!

So naturally, Sudoku puzzles are of great interest to me. Back when I was still a high school student, I wrote a Sudoku generator application that allowed users to generate and the solve the puzzle all in the application. An endless supply of fresh Sudoku for the puzzle lover.

However, Sudoku generators have been around since the very same time that the puzzle rose to sudden popularity. (In fact, the person who is largely responsible for their popularity, Wayne Gould, wrote a Sudoku generator himself.)

So for my project, I wanted to create something more complex that has never really had much time in the light. And this was how I got to my project idea: Sudoku puzzle generation in the third dimension.

Sudoku Variations

The first thing that’s highly important to understand is that there are a great many variations for three-dimensional Sudoku puzzles and there is not a single “standard” puzzle format.

Here’s just a few of the varieties I found while exploring the subject:

IsoDoku

Easily recognizable by their isometric design. They are not really designed to by playable in the third dimension, they are merely projections onto the third dimension.

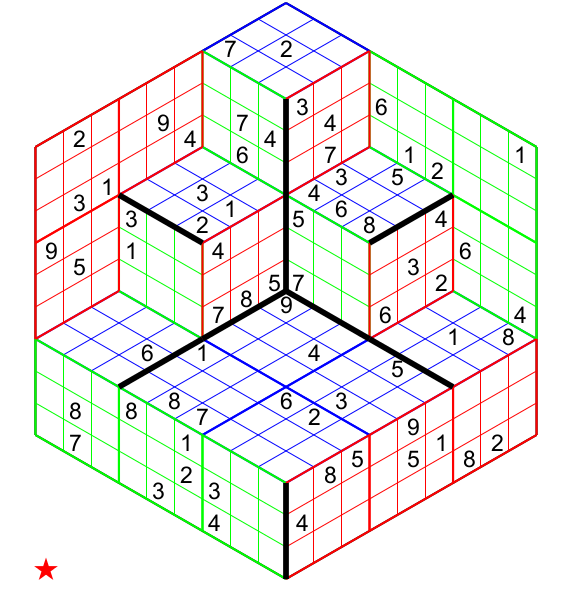
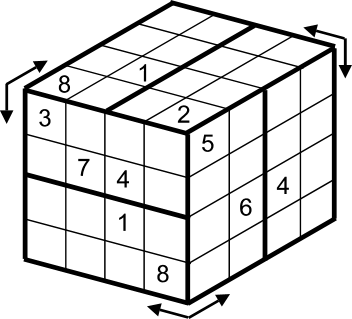
Cubic Sudoku

A true three-dimensional puzzle¹, these Sudoku puzzles are typically presented with their cubes flattened and the planes stretched vertically or horizontally.

Other Variants

These are also sometimes considered SudokuKubes or Sudoku Cubes.

The Algorithms Behind Three-Dimensional Sudoku

The generation of most types of Sudoku, including three-dimensional, is best approached in a two-step method:

• First, a valid Sudoku solution is produced with all Sudoku rules being fulfilled and met.
• Then, individual clues² are removed from the solution until the desired quantity of clues are left. All while ensuring that there is only ever one valid solution to the puzzle.

There are a few different approaches to the actual algorithms covered in the actual thesis, but the ultimately best one to generate a valid Sudoku solution is shown below:

private Sudoku3D GenSudokuSolution(int h, int r, int c, Sudoku3D puzzle){
    if (h >= size) return puzzle;
    if (r >= size) return GenSudokuSolution(h+1,0,0, puzzle);
    if (c >= size) return GenSudokuSolution(h,r+1,0, puzzle);
    List<int> neighbors = puzzle.GetNeighbors(h,r,c);
    List<int> options = Enumerable.Range(1, size).ToList<int>();
    foreach (int i in neighbors) {
        options.Remove(i);
    }
    while (options.Count != 0) {
        // select a random number from the options, remove it, and then test it
        int index = randgen.Next(options.Count);
        int testNum = options[index];
        options.RemoveAt(index);
        puzzle[h,r,c] = testNum;
        // check to see if a solution was found, else try another number in the spot
        var temp = GenSudokuSolution(h,r,c+1,puzzle);
        if (temp != null) return temp; // solution found
    }
    puzzle[h,r,c] = 0; // reset spot, no valid solution on this branch
    return null;
}

This iterates through the matrix cell by cell, picking a random number from the available numbers that are possible without breaking constraints. Then it moves forward to the next cell. In the case that a cell has no possible numbers, it backtracks to the previous cell and picks a different number.

public Sudoku3D GenSudokuPuzzle(bool newSolution = false) {
    if (solution == null || newSolution) solution = GenSudokuSolution();
    Sudoku3D tempPuzzle = solution.Clone();
    int clueCount = (int)Math.Pow(size, 3), h = 0, r = 0, c = 0;
    while (clueCount > clues){
        // continue to randomly pick indices until a spot is chosen
        while (true){
            h = randgen.Next(size); r = randgen.Next(size); c = randgen.Next(size);
            if (tempPuzzle[h, r, c] != 0) {
                tempPuzzle[h, r, c] = 0;
                break;
            }
        }
        // now check to see if puzzle still has only one solution
        if (!tempPuzzle.IsValidPuzzle()) {
            tempPuzzle[h, r, c] = solution[h, r, c];
            continue;
        }
        clueCount--;
    }
    return tempPuzzle;
}

This method will remove the value of cells one by one until the desired number of clues is reached by picking a random index to remove the value of. Then the puzzle is tested and if it has only one unique solution, it is still considered valid and proceeds to find the next index to remove.

Conclusions

Here is one of the many Sudoku puzzles my algorithm generated:

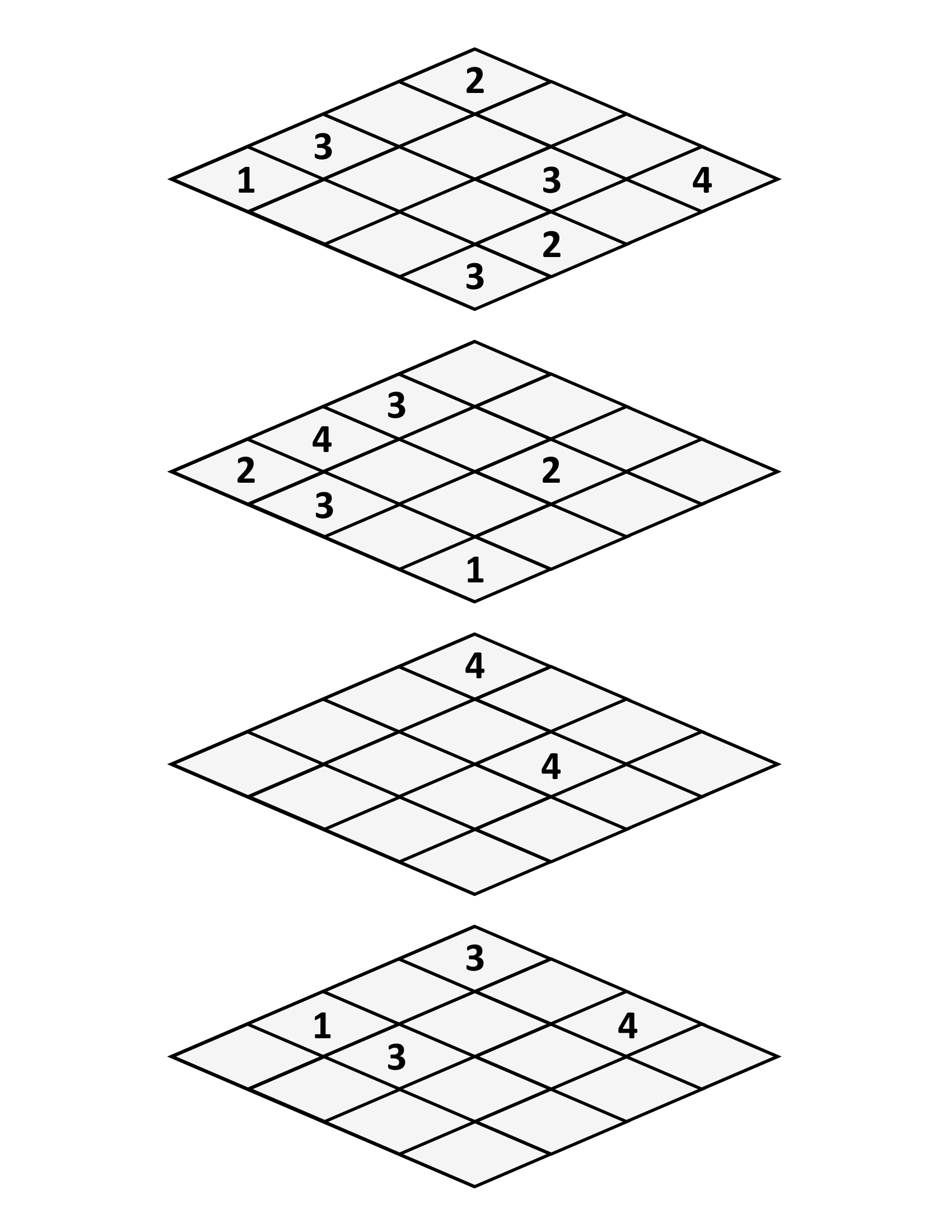
Feel free to download the image and try and solve it yourself! This one was generated on the “Hard” setting, but because its only a 4 x 4 x 4 puzzle, it shouldn’t be too difficult.³

Check out the open-sourced code that I developed for this project as well. You can find the repositories on my GitHub page.

There are hard copies available at the Albion College Library and Honors building, you can also view the online copy here.

Noah Keck

Independent Software Developer and Computer Enthusiast

Tweet Share